Како пронаћи површину пирамиде?

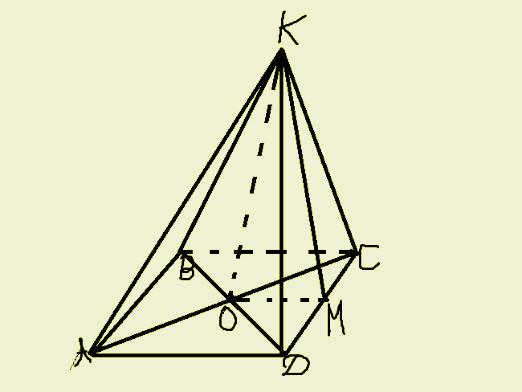
Које фигуре називамо пирамидом? Прво, то је полихедрон. Друго, произвољан полигон се налази на дну овог полиедра, а стране пирамиде (бочне стране) нужно имају облик троуглова који се конвергирају у једном заједничком вертексу. Сада, схватимо термин, схватићемо како пронаћи површину пирамиде.

Јасно је да ће се површина таквог геометријског тела састојати од суме површина базе и целокупне бочне површине.

Израчунавање површине основе пирамиде

Избор формуле за израчунавање зависи од облика основногу основи наше полигонске пирамиде. Може бити у праву, то јест, са странама исте дужине или погрешно. Размотримо обе варијанте.

На дну је регуларни полигон

Са школског курса знамо:

• квадрат квадрата ће бити једнак дужини његове стране, на квадрат;
• површина једнакостраничног троугла је једнака квадрату његове стране подељеној са 4 и помножен са квадратним кореном три.

Али постоји и општа формула за израчунавањеподручја било ког регуларног полигона (Сн): помножите периметар овог полигона (П) радиусом круга (р) уписаним у њега, а затим поделите резултат на два: Сн = 1 / 2П * р.

На дну је неправилан полигон

Шема проналаска своје области је,прво подели цео полигон на троуглове, израчунати површину сваког од њих према формули: 1 / 2а * Х (где - база троугла, х - спуштену са висином базе), сабрати све резултате.

Површина пирамиде

Сада израчунајте површину бочне површине пирамиде, тј. збир подручја свих његових бочних страна. Постоје и 2 опције.

1. Дајте нам произвољну пирамиду, тј. таква, у основи која је неправилан полигон. Затим морамо одвојено израчунати површину сваког лица и додати резултате. Пошто стране пирамида по дефиницији могу бити само троуглови, израчунавање следи горњој формули: С = 1 / 2а * х.
2. Нека наша пирамида буде права, тј. у основи је редовно полигон, а пројекција врху пирамиде је у свом центру. Затим за израчунавање подручје површине омотача (Сб) је довољна да пола производ ободу многоуглу-басе (П) до висине (х) страни (иста за све аспекте): Сб = 1/2 Р * х. Обим многоугла одређује сабирањем дужине свих његових страна.

Укупна површина регуларне пирамиде се проналази сумирањем површине његове базе са површином целокупне латералне површине.

Примери

На пример, алгебраички израчунавамо површине површина неколико пирамида.

Површина триангуларне пирамиде

У основи такве пирамиде је троугао. Према формули Со = 1 / 2а * х пронађемо површину базе. Иста формула се користи за проналажење подручја сваког лица пирамиде, такође имају троугластог облика, и добити три области: С1, С2 и С3. Површина латералне површине пирамиде је збир свих области: Сб = С1 + С2 + С3. Квадрат је искључен стране и базу, добијамо потребну површину од пирамиде: ЦБ =: Сн + СБ.

Површина квадрилатералне пирамиде

Површина латералне површине је збир 4-ектермини: Сб = С1 + С2 + С3 + С4, од којих се свака израчунава по формули површине троугла. А базна површина ће морати да се претражује, зависно од облика четвороугаона - исправно или погрешно. Укупна површина пирамиде ће поново бити добијена додавањем основне површине и укупне површине наведене пирамиде.