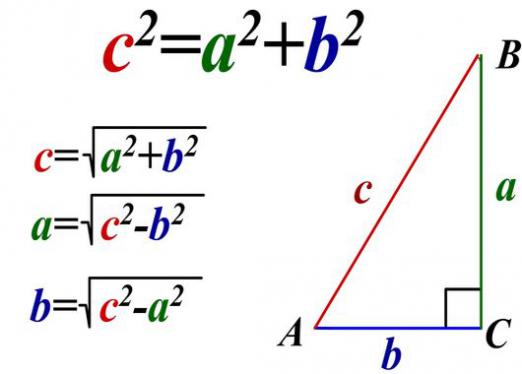
Знаци сличности троуглова

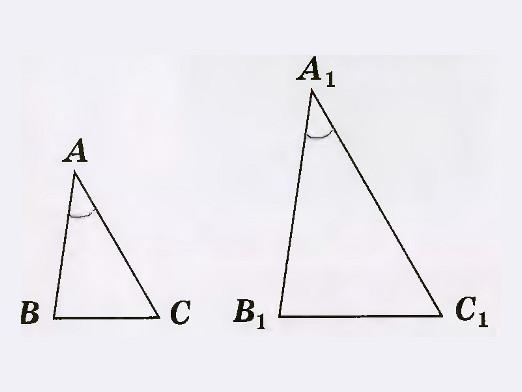
Знак сличности два троугла су такве геометријске карактеристике које нам омогућавају да утврдимо да су два одређена троугла слична једна другој, без обзира на све елементе.

Теорема 1

Први знак сличности два троугла

Троуглови су слични ако су најмање два угла у троуглу једнако два угла у другом троуглу.

Доказ.

Ако се дају два троугла: АБЦ и А1Б1Ц1, где ∠А = ∠А1 и ∠Б = ∠Б1. Тада се испоставља да су ∠Ц и ∠Ц1 једнаки. Покажимо сличност △ АБЦ и △ А1Б1Ц1.

Ако одложимо са стране ВА сегмента БА2, којасегмент ће бити једнака А1Б1, а затим нацртајте праву линију кроз тачке А2 која је паралелна са мрежног. Онда ће ова линија зауставити на тачки сегмента БЦ, која ће се звати Ц2. Дакле, троуглови и А2ВС2 А1В1С1 су: А2Б = А1Б1 изградњом ∠В1 = ∠В о стању и ∠А2 = ∠А1 као ∠А = ∠А1 о стању и ∠А2 = ∠А као и одговарајућих углова. Према лемме 1 сличних троуглова (линијом која је паралелна са једне стране троугла и пресеца друге две стране о томе, одсеца троугао, који је сличан овоме), имамо: △ АБЦ ~ троугла А2БЦ2, самим тим, троугла А1Б1Ц1 ~ троугла АБЦ. Дакле, доказана је теорема. Теореме 2 и 3 доказују слична шема.

Теорема 2

Други знак сличности троуглова.

Троуглови се сматрају сличним ако су два од њихстране једног троугла биће пропорционалне са обе стране другог троугла, респективно. Такође, мора се поштовати услов равномјерности углова између ових партија.

Теорема 3

Трећи знак сличности троуглова.

Троуглови се сматрају сличним ако се примећује услов пропорционалности три стране једног од њих на три стране друге.

Потврда 1 из теорема 1. Ако узмемо у обзир такве троуглове, онда ће њихове сличне стране пропорционално висинама које ће на сличним странама бити изостављене.

Знаци сличности правоугаоних троуглова

1. правоугаони троуглови се сматрају сличним ако су катет и хипотенуза једног од њих пропорционални нози и хипотенузи другог троугла;
2. правоугаони троуглови се сматрају сличним ако је акутни угао једног од њих једнак акутном углу другог троугла.

Знаци сличности троуглова у примјерима

Пример 1

Потребно је пронаћи дужину сегмента КП, ако је познато,да у троуглу АБЦ, дужина стране АЦ је десет, а на страни АБ постоји одређена тачка К, али АК = 2, БК = 3. Права линија се извлачи кроз тачку К, која је паралелна са АЦ. Тачка П лежи на њеној раскрсници са стране БЦ. Ово је ситуација када се користе знакови сличности троуглова. Лекција са сличним проблемом се увек налази у свакој школи. Дакле, ако у троуглу постоји равна линија, извучена паралелно са једне стране, онда се формира троугао који је сличан овом. Троугао ЦБС је сличан троуглу АБЦ. Доказано је да је угао СРС једнак углу БАЦ-а. Имајући у виду чињеницу да су то одговарајући углови који леже са паралелним РС и АЦ и сецантним АК. Поред тога, угао Б је заједнички угао, а самим тим и трећи углови су једнаки, угао БПМ и БЦА. Тако је, према теореме сличних троуглова први знак, ∠ АБЦ ∠КВР воле. Из овога следи да је РЦ / АЦ страни лежи против ∠В и ВК / ВА стране, која лежи супротно једнак ∠Р и ∠С. Дакле, проналазимо сегмент БА додавањем БК и АК. Замењујемо податке, добијамо: КР / 10 = 3/5, односно КП = 6

Пример 2

Пустите у троуглове АБЦ и А1Б1Ц1, ∠Б = ∠Б1. Странице АБ, БЦ у троуглу АБЦ су 2,5 пута веће од страна А1Б1, Б1Ц1, која је у троуглу А1Б1Ц1. Потребно је пронаћи АЦ и А1Ц1, под условом да је њихов износ 4,2 м. Решење. Према условима проблема, пишемо:

1. ∠Б = ∠Б1;
2. АБ / А1Б1 = БЦ / Б1Ц1 = 2.5 Дакле, △ АБЦ ~ △ А1Б1Ц1. Другим знаком сличности троуглова.
3. АЦ + А1Ц1 = 4,2 м. Из сличности ових троуглова добијамо резултат АЦ / А1Ц1 = 2.5 или АЦ = 2.5кА1Ц1. Ако АЦ = 2.5 к А1Ц1, онда АЦ + А1Ц1 = 2.5 к А1Ц1 + А1Ц1 = 4.2, па АЦ = 3 (м), А1Ц1 = 1,2 (м).

Пример 3

Неопходно је сазнати да ли су троуглови сличниА1Б1Ц1 и АБЦ ако цм, БЦ = 5 цм, АБ = 3, АЦ = 7 цм, Б1Ц1 = 7,5 цм, А1Б1 = 4,5 цм, А1Ц1 = 10,5 цм? Решење. БЦ / Б1Ц1 = 5 / 7.5 = 1 / 1.5 АБ / А1Б1 = 3 / 4.5 = 1 / 1.5 АЦ / А1Ц1 = 7 / 10.5 = 1 / 1.5

Према томе, трећим знаком, троуглови су слични.