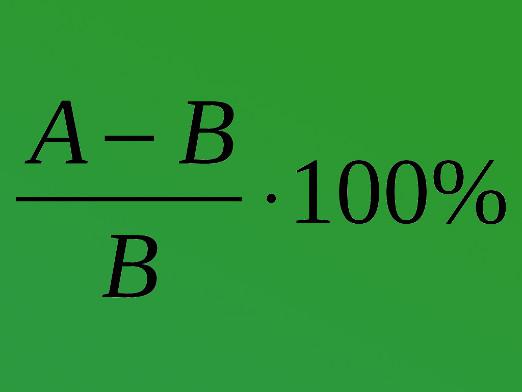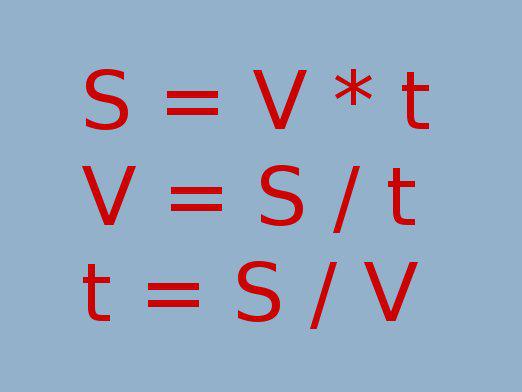Како решити проблем брзине?

Брзина, време и растојање приликом вожње су повезаниС = в * т, где је в брзина кретања, т је време потребно за кретање, а С је растојање између почетне и крајње тачке кретања. О овој основној корелацији величина, прочитајте у чланку "Како решити проблем кретања?". У наставку ћемо говорити како можете да пронађете брзину, удаљеност или време у задатку.

Решавање проблема брзине

Примери сличних проблема већ су разматрани у чланку Како пронаћи брзину, временско растојање. Разумећемо алгоритам за решавање проблема брзине и других карактеристика кретања.

Како решити проблеме: основна правила

Пре свега, морамо узети у обзир брзинукретање у таквим проблемима је константно: не постоји ни успоравање нити убрзање. Дакле, често се говори не само о брзини, већ о просјечној брзини, која је једнака в = С / т.
Потребно је пажљиво прочитати задатак и записатито је у математичком облику, и.е. уклоните све непотребне. Једнаџби није брига, то је Пит, воз или чамац, шта су урадили и зашто. Главна ствар је кретање, време, пут, брзина. То је све и треба да напишем.
Решавање проблема кретања, неопходно јеНаправите цртеж који показује цео пут, удаљеност, место састанка, итд. Затим ће карактер покрета одмах постати јасан и биће јасно шта ће бити с тим.
Немогуће је користити и метре икилометара, секунди и сати. Све количине морају имати исту димензију. Ако проблем каже да је један објекат био на путу 10 сати, а друга половина дана, потребно је да је преведете на сат.

Пример решавања проблема брзине

Размотрите проблем. Удаљеност од града до села је 45 км. Пешак је ушао у град са брзином од 5 км / х из села. Сат сат касније, бициклиста са брзином од 15 км / х отишао је да га упозна са града до села. Које ће бити у близини села у време састанка?

Пажљиво прочитамо и напишемо услове проблема:

С = 45 км
в1 = 5 км / х.
в2 = 15 км / х.
т1 - т2 = 1 х - пешак је напустио сат раније, тада, пре него што је састанак прошао сат времена дуже.
с1 =? с2 =? - Да сазнамо ко је био ближе селу, треба знати пут обоје.

Направићемо цртеж. Цртежемо линијски сегмент, на крај који означава Село (Ц) и Град (Д).

Између тачака Ц и Д, растојање је 45 км. Пешак је отишао сат времена раније - ставили смо тачку П близу точке П, ово је место до којег је стигао у сат. Близу средине поставили смо још једну тачку Б - место састанка. Морамо знати растојање ЦБ и ГВ.

Из цртежа се види: