Како пронаћи сине?

Проучавање геометрије помаже развити размишљање. Овај предмет неопходно улази у припрему школе. У животу, знање о овој теми може бити згодно - на пример, приликом планирања стана.

Из историје

Унутар курса геометрије се такође проучава тригонометрија, која истражује тригонометријске функције. У тригонометрији проучавамо сине, косине, тангенте и котангенте угла.

Али за сада ћемо почети са најједноставнијим - сине. Размотримо детаљније први концепт - сине углова у геометрији. Шта је сине и како га пронаћи?

Концепт "синусног угла" и синусоида

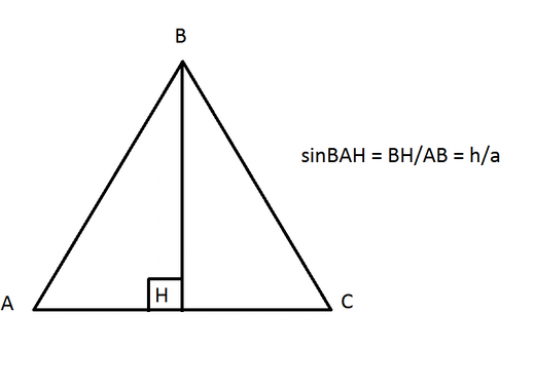
Синус угла је однос вредностисупротну ногу и хипотенузу правоуглог троугла. Ово је директна тригонометријска функција, која се у слову означава као "син (к)", где је (к) угао троугла.

На графикону, синус угла означава синусоид ωњегове карактеристике. Синусни талас личи на континуирану таласасту линију која лежи у одређеном оквиру на координатној равни. Функција је чудна, стога је симетрична око 0 на координатној равни (она оставља порекло координатне референце).

Подручје дефиниције ове функције лежи укреће се од -1 до +1 на картезијанском координатном систему. Период функције синусног угла је 2 Пи. То значи да се сваки поновљени 2 Пи понавља и синусни талас пролази кроз цео циклус.

Једначина синусоида

• син к = а / ц
• где је а катет супротан углу троугла
• ц - хипотенуза правог троугла

Својства углова сина

1. син (к) = син син (к). Ова карактеристика показује да је функција симетрична, а ако поставимо вриједности к и (-к) на обе стране координатног система, онда ће ординати ових тачака бити супротни. Оне ће бити једнако једнаке.
2. Друга карактеристика ове функције је та,да се граф функције повећава на интервалу [-Π / 2 + 2 Пн]; [П / 2 + 2Пн], где је н сваки интегер. Смањење сина угла ће се посматрати на сегменту: [П / 2 + 2 Пн]; [3П / 2 + 2Пн].
3. син (к)> 0, када к лежи у опсегу (2πн, Π + 2πн)
4. (к) <0, када је к у опсегу (-П + 2Пн, 2Пн)

Вредности сине углова су одређене посебнимтабеле. Такве табеле су створене како би се олакшало израчунавање сложених формула и једначина. Лако се користи и садржи не само функције син (к), већ и вредности других функција.

Штавише, табела стандардних вредности овихФункције укључене у обавезно студији меморије, као таблицу множења. Ово се посебно односи на наставу из физике и математике. Табела се могу видети вредности основних тригонометријске углова користе су 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 и 360 степени.

вредност угла α (степени)	0	15	30	45	60	75	90	120	135	150	180	270	360
Вредност угла α у радијанцима (у смислу броја пи)	0	π / 12	π / 6	π / 4	π / 3	5π / 12	π / 2	2π / 3	3π / 4	5π / 6	π	3π / 2	2π
грех (синус)	0	√3-1 / 2√2	1/2	√2 / 2	√3 / 2	√3 + 1 / 2√2	1	√3 / 2	√2 / 2	1/2	0	-1	0

Постоји и табела која дефинира вредноститригонометријске функције нестандардних углова. Користећи различите табеле, лако можете израчунати синусни, косинусни, тангентни и котангентни од неких углова.

Са тригонометријским функцијама се састављајуједначине. Лако је ријешити ове једначине ако знамо једноставне тригонометријске идентитете и функције редукције, на пример, као што је син (н / 2 + к) = цос (к) и други. За такве духове направљен је и засебан стол.

Како пронаћи сине под углом

Када је задатак пронаћи синус угла и условом, имамо само косинус, тангентни или котангентни угао, лако можемо израчунати жељену помоћ тригонометријских идентитета.

• грех²к + цос²к = 1

На основу ове једначине можемо пронаћи и синус и косинус, у зависности од тога која је вредност непозната. Добијамо тригонометријску једначину са једним непознатим:

• грех²к = 1 - цос²к
• син к = ± √ 1 - цос²к
• цтг²к + 1 = 1 / син²к

Из ове једначине можете пронаћи вриједност сине, знајући вриједност угла котангентне. За једноставност замијените грех²к = и, а затим добијате једноставну једначину. На пример, вредност кокангента је 1, а затим:

• 1 + 1 = 1 / и
• 2 = 1 / и
• 2и = 1
• и = 1/2

Сада извршите обрнуту замену игре:

• грех²к = ½
• син к = 1 / √2

Пошто смо узели коцкангентну вредност за стандардни угао (45⁰), добијене вредности могу се проверити из табеле.

Ако вам се дода вредност тангенте и морате пронаћи сине, други тригонометријски идентитет ће помоћи:

• тг к * цтг к = 1

Од овога следи:

• цтг к = 1 / тг к

Да би пронашли сине нестандардног угла, на пример, 240⁰, неопходно је користити формуле за смањење углова. Знамо да π одговара 180⁰. Стога, изражавамо нашу једнакост помоћу стандардних углова распадом.

• 240⁰ = 180⁰ + 60⁰

Морамо наћи следеће: грех (180⁰ + 60⁰). У тригонометрији постоје формуле редукције, које су у овом случају корисне. Ово је формула:

• син (π + к) = - син (к)

Стога, синус угла од 240 степени једнак је:

• грех (180⁰ + 60⁰) = - син (60⁰) = - √3 / 2

У нашем случају, к = 60 и П, односно 180 степени. Вредност (-√3 / 2) смо нашли из табеле вредности функција стандардних углова.

На тај начин, нестандардни углови се могу проширити, на примјер: 210 = 180 + 30.

У уџбеницима и на Интернету можете се срести многиФормуле за израчунавање тригонометријске једначине - одузимање, сабирање, дељење и производ тригонометријских функција различитих углова међусобно у степену вазнесења и претварање једне функције на другу једноставним идентитетом и многе друге радње.

За више информација о синусима и косинусима, погледајте:

• Шта је сине
• Како пронаћи сине ако је косинус познат