Како изградити вектор?

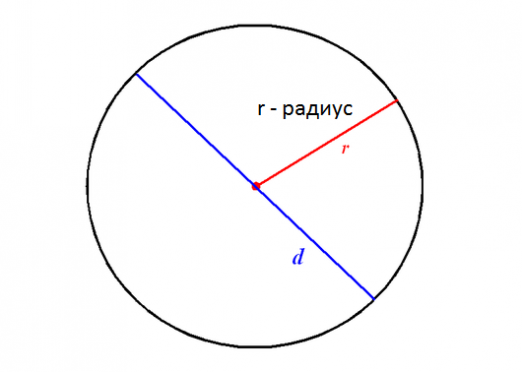
Вектор се обично назива сегмент који имаодређени правац. И почетак и крај вектора имају фиксну позицију, помоћу кога се одређује правац вектора. Размотримо детаљније како се конструише вектор са датим координатама.
- Нацртајте координатни систем (к, и, з) у простору, означите поједине сегменте на осама.
- Одвојите на двије осовине потребне координате, извуците од њих тачкане линије које су паралелне са осама, до раскрснице. Научите тачку раскрснице, коју морате повезати тачкастом линијом са пореклом.
- Нацртајте вектор од поријекла до резултирајуће тачке.
- Одвојите на трећој оси жељени број, кроз ову тачку нацртајте тачкасту линију која ће бити паралелна конструисаном вектору.
- Од краја вектора за спровођење испрекидана линија паралелно са треће осе до раскрснице са линије последњег пасуса.
- На крају, повежите порекло и добијену тачку.
Понекад је потребно направити вектор, који ће бити резултат додавања или одузимања других вектора. Дакле, сада ћемо размотрити операције са вектори, научићемо како их додавати и одузети.
Операције на вектору
Геометријски вектори се могу додатина неколико начина. На пример, најчешћи метод вектора Поред генерално троугаони. За додавање два вектора према овом правилу, неопходно је уредити вектори паралелно, тако да почетак првог вектора да се поклопи са другом крају, трећа страна троугла ће се добити од стране векторски збир.
Такође можете израчунати суме вектора по правилупаралелограм. Вектори треба да започну из једне тачке, паралелно сваком вектору, морате извући линију тако да се добије паралелограм добијен. Дијагонала конструисаног паралелограма ће бити збир ових вектора.
Да одузмемо два вектора, морамо додати првовектор и вектор који је супротно другом. У ту сврху се користи генерално троугао, који има следећу формулацију: разлика вектори се преносе тако да почну подударају, је вектор чији почетак се поклапа са крајем умањилац вектора, као и крај редукованог вектора.