Додатна својства

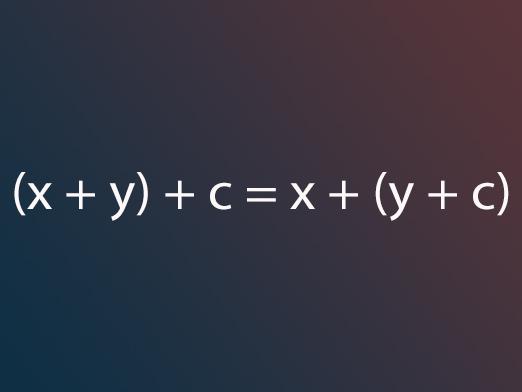
Постоје три особине додавања бројева,које се користе за решавање математичких проблема, како у једноставној тако иу комплексној математици. Путујућа, комбинована и дистрибуирајућа својства имају своје специфичности и користе се само када се бројеви комбинују и умножавају, а ни у једном случају, ни у једној другој аритметичкој операцији.

• Комбиновање својства додавања бројева значи(к + и) + ц = к + (и + ц) је тачно за било који од бројева к, и и ц који мора бити додан. Својства комбиновања која се користи у множењу бројева значи да је за било који од бројева к, и и ц једнакост (ки) ц = к (иц) тачна.
• За покретну имовинудодавање било ког броја бројева к и и, означава да се ови бројеви могу преуређивати у било којем правцу, да их групишу у групе на начин који је прихватљив у одређеном случају, а резултат се неће променити. Имовина померања додатка означава да се сума добијена када се додају два броја не мења ако се ови бројеви замењују. Користи се следећа једначина: к + и = и + к.
• Расположивост додавања дозвољавадодајте бројеве, према овој једначини: (к + и) + ц = к + (и + ц). Иста особина се користи у множењу у складу са сљедећом једначином: (ки) ц = к (иц). Дистрибутивна својина примјењује се не само када је потребно умножити збир два сума, већ и сума од три или више термина. У овом случају, једнакост држи: к (и + ц + д) = ки + кц + кд, без обзира на то што су бројеви к, и, ц и д.