Како пронаћи периметар троугла?

Често математички проблеми захтевају дубокуанализа, способност тражења решења и одабирање правих изјава, формула. У оваквом раду није тешко збунити. А ипак постоје проблеми чије се рјешење сведе на употребу једне формуле. Такви проблеми укључују питање како пронаћи периметар троугла.
Хајде да размотримо основне формуле за решење овог проблема у вези са различитим врстама троугла.
- Главно правило за проналажење периметратроугао је следећа изјава: периметар троугла је једнак суму дужине свих његових страна. Формула П = а + б + ц. Овде а, б, ц су дужине страница троугла, а П је његов периметар.
- Постоје посебни случајеви ове формуле. На пример:
- ако је проблем питање како пронаћи периметар правоугаоног троугла, онда можемо користити и класичну формулу (погледати § 1) и формулу која захтева мање података: П = а + б + √ (а2+ б2). Овде а, б су дужине ногу правог троугла. Лако је видјети да се трећа страна (хипотенуза) замјењује изразом из Питагореове теореме.
- Из периода проналазног троугла налази се П = 2 * а + б. Овде а је дужина стране троугла, б је дужина његове базе.
- Да бисте пронашли периметар једнакостраничног (или регуларног) троугла, израчунајте вредност израза П = 3 * а, где је а дужина стране троугла.
- за решавање проблема у којима се појављују такви троуглови, корисно је знати следећу изјаву: однос периметра је једнак коефицијенту сличности. Погодно је користити формулу
П (ΔАБЦ) / П (ΔА1Б1Ц1) = к, где је ΔАБЦ ~ ΔА1Б1Ц1, а к је коефицијент сличности.
Пример:
С обзиром на ΔАБЦ са странама 6, 8 и 10 и ΔА1Б1Ц1Са стране 9, 12. Познато је да је угао Б једнак углу Б1. Пронађите периметар троугла А1Б1Ц1.
Решење
- Нека АБ = 6, БЦ = 8, АЦ = 10; А1Б1= 9; Б1Ц1= 12. Имајте на уму АБ / А1Б1= БЦ / Б1Ц1, т. 6/9 = 8/12 = 2/3. И хипотезом Б = Б1. Ови углови су између страна АБ, БЦ и А1Б1, Б1Ц1респективно. Закључак - према другом критеријуму сличности троуглова, ΔАБЦ ~ ΔА1Б1Ц1. Коефицијент сличности је к = 2/3.
- Нађимо по формули тачке 1 П (ΔАБЦ) = 6 + 8 + 10 = 24 (јединице). Могуће је користити формулу тачке 2а, пошто Питагорејска теорема доказује да је ΔАБЦ правоугаона.
- Из тачке 2д следи да је П (ΔАБЦ) / П (ΔА1Б1Ц1) = 2/3. Стога П (ΔА1Б1Ц1) = 3 * П (ΔАБЦ) / 2 = 3 * 24/2 = 36 (јединице).
Прочитајте више:

Како пронаћи периметар паралелограма?
Како пронаћи периметар дијаманта?

Како пронаћи периметар полигона?

Како пронаћи периметар квадрата?

Како пронаћи периметар правоугаоника?

Како пронаћи периметар и област?

Како пронаћи периметар и површину правоугаоника?

Који је периметар?
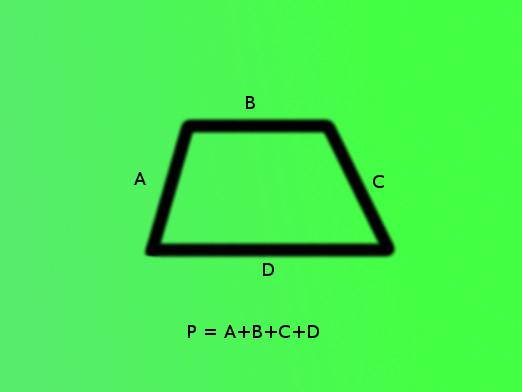
Како пронаћи периметар?

Који је периметар троугла?