Како пронаћи област цифре?

Знајте и будите у стању да израчунате различите областиподаци су потребни не само за решавање једноставних геометријских проблема. Не радите без оваквог знања и приликом састављања или провере процјена за поправку просторија, рачунајући број потребних залиха. Па, хајде да схватимо како да нађемо подручја различитих фигура.

Област

Дио плана затвореног у затвореном конту назван је област ове равни. Подручје је изражено бројем квадратних јединица у њој.

Да бисте израчунали површину основних геометријских облика, морате користити исправну формулу.

Подручје троугла

Нотатион:

• С је потребна област,
• а, б, ц су дужине страница троугла,
• х је висина жељеног троугла,
• γ је угао између стране а и стране б,
• р је полупречник круга (уписан у троугао),
• Р је радијус круга (описан око троугла),
• п је половина периметра троугла.

1. Ако је познато х, а, жељени површина троугла се дефинише као производ дужине троугла стране и висина се спушта ка овој страни, подељена на пола: С = (А · х) / 2
2. Ако су а, б, ц познате, онда је потребна областизрачунава херонова формула: квадратни корен узети производа пола ободу троугла и три разлике пола и обим сваке стране троугла: С = √ (п · (п - а) · (п - б) · (п - ц)).
3. Ако су познате а, б, γ, онда је површина троугла дефинисана као половина производа са 2 стране помножена с вриједношћу угла синуса између ових страна: С = (а · б · син γ) / 2
4. Ако знамо А, б, ц, Р, потребну област је дефинисана као производ дужине свих поделе странама троугла у четири полупречника ОПИСАНИ КРУГ: С = (А · Б · Ц) / 4Р
5. Ако знамо п, р, одговарајући подручје троугла дефинисаног множењем половину периметра на полупречнику круга уписаног у њој: С = п · р

Трг квадрата

Нотатион:

• С је потребна област,
• а је дужина стране,
• д је дужина дијагонале.

1. Ако је страна позната, онда је површина ове фигуре дефинисана као квадрат са дужином стране: С = а²
2. Ако је д познато, квадрат квадрата је дефинисан као пола квадрата дужине његове дијагонале: С = д²/ 2

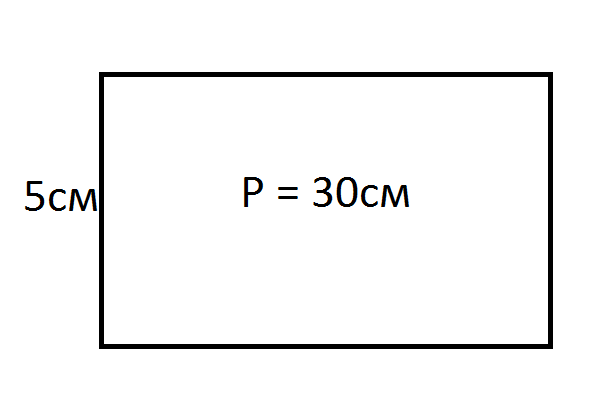
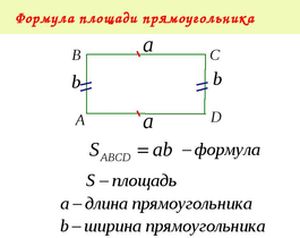
Површина правоугаоника

Нотатион:

• С је подручје које треба одредити,
• а, б су дужине страница правоугаоника.

1. Ако су а, б познате, онда је површина овог правоугаоника одређена производом дужине две стране: С = а · б
2. Ако дузине страна нису познате, тада област правоугаоника мора бити подељена у троуглове. У овом случају, површина правоугаоника је дефинисана као збир подручја његових конститутивних троуглова.

Подручје паралелограма

Нотатион:

• С је потребна област,
• а, б су дужине страна,
• х је дужина висине овог паралелограма,
• д1, д2 су дужине две дијагонале,
• α је угао између страна,
• γ је угао између дијагонала.

1. Ако су а, х познате, онда се жељена површина одређује множењем бочних дужина и висине која се пада са ове стране: С = а · х
2. Ако су а, б, α познате, онда је област паралелограма одређена множењем дужине страница паралелограма и синусне вредности угла између ових страна: С = а · б · син α
3. Ако знамо д₁, д₂, γ, онда је област паралелограма дефинисана као половина производа дијагоналне дужине и синусна вриједност угла између ових дијагонала: С = (д₁· Д₂· Синγ) / 2

Диамонд Скуаре

Нотатион:

• С је потребна област,
• а је дужина стране,
• х је дужина висине,
• α је мањи угао између две стране,
• д1, д2 су дужине две дијагонале.

1. Ако су а, х познате, онда је област ромба одређена множењем дужине стране дужине висине која се спусти на ову страну: С = а · х
2. Ако су а, α познати, онда је ромбична област одређена множењем квадрата дужине стране сине угла између страна: С = а²· Син α
3. Ако знамо д₁ и д₂, онда је неопходна област дефинисана као половина производа дужине дијаманата ромба: С = (д₁· Д₂) / 2

Трапезијум подручје

Нотатион:

• С је потребна област,
• а, б - дужине 2 базе трапезијума,
• ц, д су дужине леве и десне стране трапезоида,
• х је висина трапезоида,

1. Ако су а, б, ц, д познате, онда је тражена површина одређена формулом: С = (а + б) / 2 * √ [ц²- (((б-а)²+ ц²-д²) / (2 (б-а))²].
2. За познато а, б, х, тражена површина је дефинисана као производ од половине збирке база и висине трапезијума: С = (а + б) / 2 · х

Површина конвексног четвороугаона

Нотатион:

• С је потребна област,
• д₁, д₂ - дужине дијагонала датог четвороугаона,
• α је угао између дијагонала,
• п = (а + б + ц + д) / 2 је половина периметра конвексног четвороугла,
• а и б, ц и д су дужине сваке стране конвексног четвороугла,
• θ = (α + β) / 2 је половина збирке два супротна угла конвексног четвороугла,
• р је полупречник круга уписаног у конвексни четверострук.

1. Ако знамо д₁, д₂, α, онда је површина конвексног четвороугла дефинисана као половина производа дијагонала четвероструког помноженог угао синуса између ових дијагонала: С = (д₁· Д ₂· Син α) / 2
2. Са познатим п, р конвексан четвороугао дефинисану као производ половине ободу четвороугла од полупречника круга уписаног у четвороугла: С = п · р
3. Ако су а, б, ц, д, θ познате, онда је површина конвексногКвадрилатер је дефинисан као квадратни коријен производа различитости полперпериметра и дужине сваке стране минус производ дужине свих страна и косинусног квадрата од половине збирке два супротна угла: С² = (п - а) (п - б) (п - ц) (п - д) - абцд · цос²((α + β) / 2)

Круг подручја

Нотатион:

• С је потребна област,
• р је дужина радијуса,
• д је дужина пречника.

Ако је р познат, онда је жељена површина дефинисана као производ броја π радиусом на квадрату: С = π р²

Ако је познато д, онда је површина круга дефинисана као производ броја π квадратом пречника, подељеног са четири: С = (π · д²) / 4

Подручје сложене фигуре

Сложени се могу поделити на једноставне геометријске фигуре. Подручје сложене фигуре дефинише се као збир или разлика у саставним областима. Размотримо, на примјер, прстен.

Ознака:

• С је подручје прстена,
• Р, р су полупречници спољног обима и унутрашње, односно,
• Д, д су пречници спољног круга и унутрашњег обода, респективно.

Да бисте пронашли подручје прстена, неопходно је узети подручје

мањи круг. С = С1-С2 = πР²-πр² = π (Р²-р²).

Дакле, ако су Р и р познати, онда је површина прстена дефинисана као разлика квадрата полупречника спољашњих и унутрашњих кругова помножених са бројем пи: С = π (Р²-р²).

Ако је познато Д и д, подручје прстен се дефинише као четвртине разлике квадрата пречника спољашње и унутрашње лукове, помножено пи: С = (1/4) (Д²-д²) π.

Подручје осенчене фигуре

Претпоставимо да постоји још један (Б) (мањи) унутар истог квадрата (А), а требамо наћи сјењену шупљину између фигура "А" и "Б". Хајде да кажемо "оквир" на малом квадрату. Да бисте то урадили:

1. Налазимо подручје слике "А" (израчунато по формули за проналажење квадрата квадрата).
2. Слично томе, пронађемо површину слике "Б".
3. Одвојимо површину "Б" из подручја "А". И тако добијамо подручје осенчене фигуре.

Сада знате како пронаћи делове различитих облика.